📓 Introduction to Trees

In this lesson, we'll learn about the basics of tree data structures. There are actually many different kinds of tree data structures, but we will focus on a few common ones. In this lesson, we'll cover general trees. Later in this section, we'll cover binary trees and binary search trees. We will also cover graphs, tries, and heaps in future sections.

General Trees

In computer science, a tree is a data structure that looks like an upside-down tree. We could also say it looks like the root system of a tree — however, we'll see in a moment why we describe it as an upside-down tree instead. Unlike data structures such as arrays and linked lists, which store data in a linear fashion, trees are non-linear data structures.

You've probably used a tree structure before, especially if you're interested in genealogy — a family tree is an example of a tree structure. While there are key differences in the way a family tree is structured, there is also a key similarity — family trees are used to convey data about relationships between people in a family. We can always trace our way through a family tree to find the exact relationship between two people — whether that is a great-great-grandparent or a fourth cousin. In the same way, we can traverse a tree structure to find relationships between different pieces of data.

Here is an example of a general tree structure.

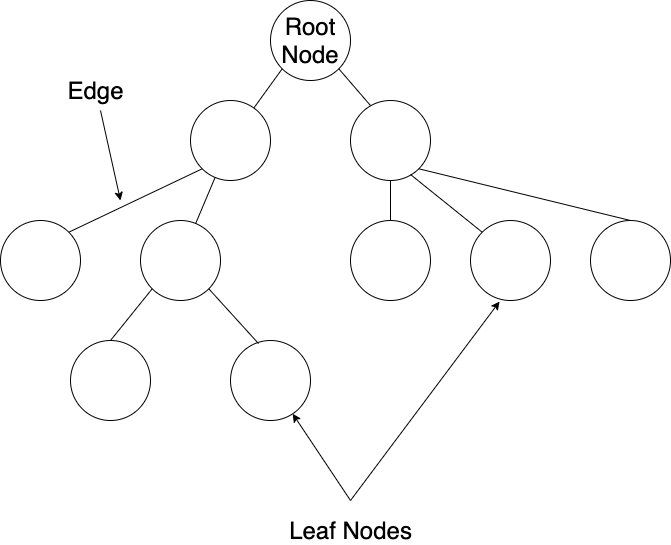
A tree consists of connected nodes. Each connection between nodes is called an edge. Parent nodes can have many child nodes, but a child node can have only one parent. A tree structure will have a single root node which is either directly or indirectly the parent of all other nodes in the tree. As you can probably guess, the root node is never a child node to other nodes. Finally, child nodes that don't have any children of their own are called leaf nodes. It should be clear how this is similar to an upside-down tree — the leaf nodes are at the bottom while the root node is at the top.

Also, the above tree has a height of 4, which we can determine by counting from the top root node all the way down to the furthest leaf node.

We can also break up a tree into a series of subtrees or smaller trees. For instance, the image below shows a subtree inside the larger general tree.

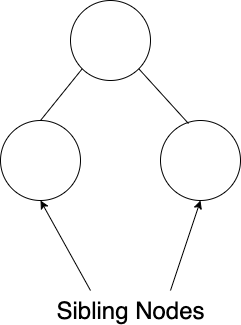
In this image, we also show two sibling nodes. Nodes that share the same direct parent are siblings. It's important to note, however, that sibling nodes aren't connected by edges.

Why is that important? Well, we can traverse a general tree structure because all nodes are linked, either directly or indirectly. However, to traverse between sibling nodes, we need to do so indirectly via their shared parent node. We will explore traversing trees further in future lessons.

Each node also has a key.

In a general tree, nodes don't necessarily have to be ordered in any specific way. However, in other types of trees, we'll find that the way nodes are placed is very important.

Can you think of a specific example of a tree structure we use every day at Epicodus? Hint: We can use the command cd to navigate through it.

If you guessed a file structure, you are correct. Whenever we navigate through folders on a computer, we are traversing through a tree structure. We can navigate up to the root node — the root directory in our computer. We can navigate between siblings, but only if we first cd up to a shared parent node. We can navigate to any directory or file on our machines via this traversal. Just from this small example, we can see that general trees are an essential part of our daily lives as developers. However, the importance of trees in computer science extends far beyond the file structures on our machines.