📓 Heaps
In this lesson, we'll cover heaps, a special kind of data structure that's most commonly used for allocating memory. This type of data structure isn't as directly relevant to what we've covered at Epicodus — after all, languages like JavaScript handle memory allocation for us. However, we are benefiting constantly from heaps all the same. Our machines use them constantly to allocate memory. JavaScript's V8 engines uses them to store variables as needed. And a basic understanding of this data structure is still an important computer science concept.
We can visualize a heap as a kind of binary tree that's organized either from lowest to highest or highest to lowest. Let's take a look at both types.
The first illustration shows a min heap. A min heap, as you might guess, has values organized from lowest to highest.
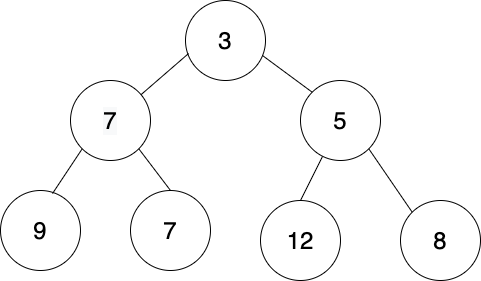
While heaps look like binary trees, note how they are different from binary search trees — a right child doesn't need to be greater than a left child. Also, as you can see from the illustration, a heap can have duplicate values while a binary search tree can not.
Now let's look at a max heap, where values go from highest (in the root node) to lowest (in the leaf nodes).
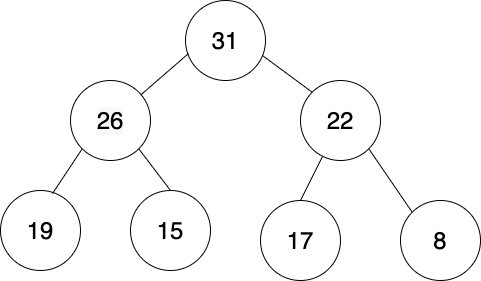
There are two more very important rules about heaps:
-
They must always be complete binary trees. That means that all but the bottom row of tree must be filled. In other words, when adding or removing things from a heap, we need to make sure that we fill all rows completely (other than the bottom row).
-
They must always be filled from left to right. It doesn't matter whether values or higher or lower than their siblings (just that they are higher or lower than their parents and children depending on whether it's a min or max heap).
For instance, this isn't a heap:
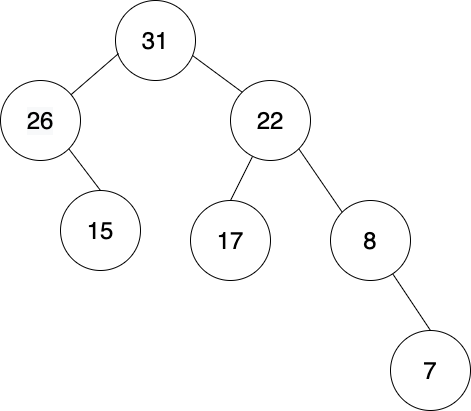 .
.
Remember, every row except for the bottom row must be filled. In this case, there is an incomplete row that's not the bottom row. If we moved the 7 node into the incomplete space, this would be a heap.
Also, since all rows must be filled left to right, another key rule is broken here as well.
When are heaps useful? Well, heaps are especially useful in situations where we regularly need to remove the lowest or highest value. If we regularly need to remove the lowest value, we'd use a min heap. If we regularly need to remove the highest value, we'd use a max heap. That's because it's very easy to find the lowest/highest value in a heap — just check the root node!
Because of the rules of a heap, keeping the shape of the tree consistent is challenging. When we remove a value from a heap, such as when we remove the root node, we need to restructure the heap to fill the root node again while following both key rules of heaps: that rows must be complete where possible and that rows must be filled from left to right. The same challenges apply when we add a value to a heap. Generally, when a value is added to a heap, it is first added to the bottom, left-most free spot and then we'd use an algorithm to allow it to bubble up to a spot where it's numerical value follows the rules of that particular heap.
We are not going to cover algorithms for adding and removing values from a heap. For now, it's enough to just know the basics about this important data structure.
If you'd like to learn more about heaps, including the basic principles of adding and removing values from a heap, check out Gayle Laakmann McDowell's video on this topic. McDowell is author of Cracking the Coding Interview. While her code examples use Java, she explains heaps very clearly and the basics of how algorithms used to add and remove values from heaps is very clear.