📓 Building Graphs Part 1
Imagine we've been hired to work on an application that keeps track of friendships between people. This kind of application has many use cases — after all, this is the foundation of many social networks. Remember that a graph is just another way of depicting a network. So when we think about portraying a social network, we could also call it a social graph. So let's get to work! In our application, we should be able to do the following:
- Add people (nodes) to the social network. To keep it simple, they will only have a
nameproperty. - Add friendships between people (edges between nodes). These will be unweighted and undirected.
- Remove nodes from the social network. Some people may want to revoke their accounts.
- Remove edges from the social network. Sadly, some people may want to end their friendships.
This graph will not be a connected graph. A connected graph is one where a potential path exists between every single node in the graph. However, in an actual social network, we can't assume that everyone knows each other. Our social network could look like this:
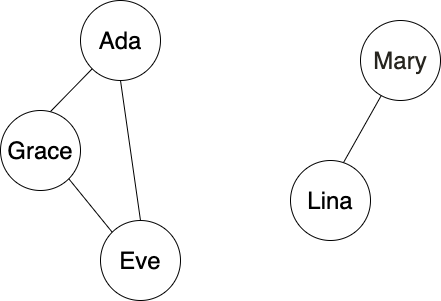
In the image above, Ada, Grace and Eve are friends. However, no one in this group is friends (yet) with Mary and Lina, who have their own friend group.
Once we've completed all of the above functionality, we'll be ready to explore two algorithms:
- An algorithm for checking the reachability between two nodes. For instance, we can reach Ada via Eve or Grace but not via Mary or Lina. In a social network trying to bring different groups together, knowing the reachability between two nodes could be very useful. For instance, in a social network working to mobilize voters, it might be useful to see if various people in a city are connected or not. If not, introducing them could allow them to work together and better mobilize. We will walk through the process of writing this algorithm.
- An algorithm checking the shortest path between two nodes. In the chart above, the shortest path between all reachable nodes is just one edge but a more complex social network would have paths of varying lengths. In this way, we can check the degrees of separation between two people in the network. This could have many uses in a real-world application as well. For instance, in a professional network like LinkedIn, it might be useful to see your closest connection at a place you hope to work — and how you are connected. Or you might want to design a friend finder that automatically recommends connecting with friends of friends — which, in the parlance of graphs, would be all adjacent nodes of a node. We won't walk through this method — instead, you will have the opportunity to use one of the algorithms we discuss in order to solve this problem on your own.
You can probably imagine all kinds of ways to build this application out further. Imagine, for instance, that we decided to weight edges based on the number of social interactions between two nodes. We could then determine their overall connectivity (and perhaps even make assumptions about how close they are as friends). And you can likely also imagine all kinds of other use cases for graphs besides social networks ranging from transportation networks to HR applications to business applications tracking international trade.
In the next lesson, we'll actually start building our application.